* 이 포스트는 컴퓨터 비젼에 대한 개인 학습용으로 작성한 포스트입니다.
Shape of Shading
Shading : Continuous image brightness variation due to shape variations
- Shape from Shading(SFS) : 3D shape recovery from a single image
- Photometric Stereo (PS) : 3D shape recovery from multiple images with different illuminations
가정 : orthographic camera projection (모든 빛이 평행하게 들어온다 가정)
그리고 반사된 빛이 그대로 Image plane에 맺힌다 가정한다 (E = L)

결국, Image plane에 맺힌 E(x,y)를 통해 normal vector n을 찾고, $\varphi(x,y)$를 복구하는 문제이다.
Reflectance Map
normal vector를 구하기 위해 $delta z$를 정의할 필요가 있다. 편미분을 통해 다음과 같이 나타낸다.
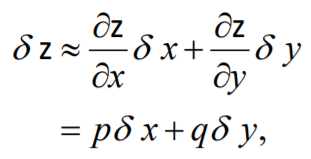
그러면 normal vector는 다음과 같다.

이를 통해, surface orientation과 brightness의 관계를 보여주는 Reflectance Map을 구할 수 있다.
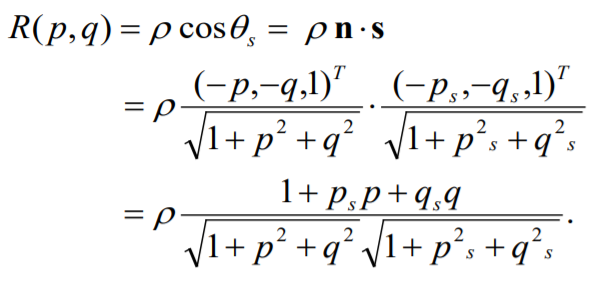
Shape from Shading Formulation
R을 통해 shape을 추정하기 위해 다음과 같은 가정을 사용한다.
- light source가 매우 먼 거리에 있다.
- Orthographic camera projection
- 물체에서 반사된 빛이 입사되지 않음
- Lambertian surface
하지만 이 문제를 푸는데 가장 큰 문제가 있는데,
아래는 p, q에 따른 Equal brightness contour이다.
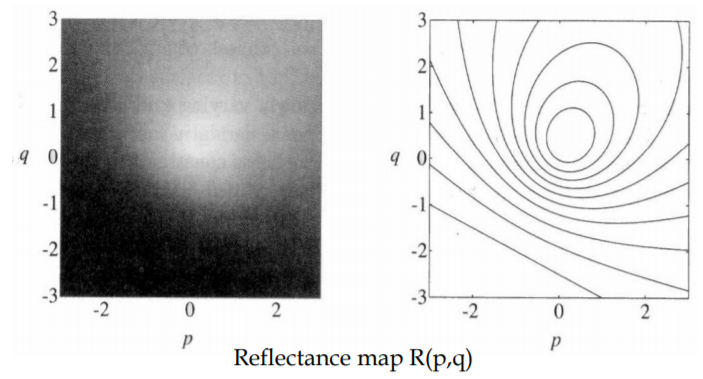
같은 R에 해당되는 p, q가 여러개이기 때문에 하나의 값으로 normal vector를 단정하기 어렵다.
Horn's Approach
위의 문제를 풀기 위해 에너지를 정의하고 이를 minimize하는 문제로 변환한다.
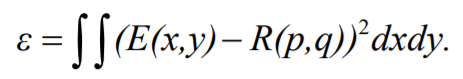
이것도 유일한 값이 도출되지 않기 때문에 다음과 같은 regularization term을 추가한다.

이를 Euler equation을 통해 iterative relation으로 바꾼다.
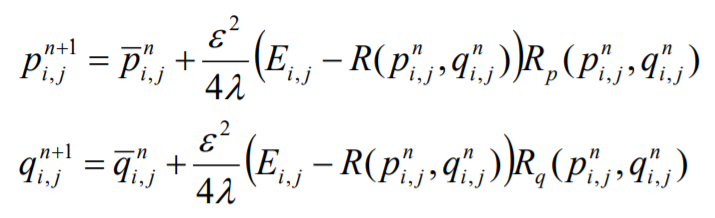
최종적으로 구해진 p, q값을 토대로 적분하면 z를 구할 수 있다.

그 전에, 구해진 p, q가 integrability를 가지기 위해 regularization term을 다음과 같이 설계한다.

Photometric Stereo
Photometric Stereo문제는 SFS 문제보다 쉬운데, 위에서 설명했던 bright contour를 보면,

하나의 surface에 대해 3개의 irradiance 정보만 있으면 그 교점으로 쉽게 p, q를 찾을 수 있다.
여러개의 image에 대해 다음과 같이 matrix로 표현할 수 있고, least square solution을 통해 구할 수 있다.

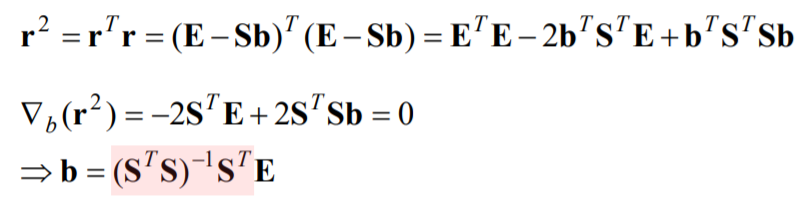

Uncalibrated Photometric Stereo
하지만 위의 모든 방법은 조명 방향을 알 수 없는 경우 구할 수가 없다.

위의 관측된 I에 대해 B와 S를 추정해야하는 문제로 넓어진다. 하지만 이 경우의 B, S는 unique하지 않다.
이를 풀기 위해 SVD를 이용하고 3X3 matrix로 근사한다.

하지만 구한 $B^*$는 실제 surface를 나타내지 않는다. 실제 surface로 변환해주는 matrixs는 GBR(Generalized Bas-Relief) matrix이다.


In Real World
위의 방법으로 surface를 recovery할 수 있지만, 다양한 원인들로 인해 문제를 풀기 복잡해진다.
- Diffuse light sources
- Interreflections between surfaces
- Varying surface albedo
- Non lambertian reflections
- Shadows (cast)
'Basic Learning > Computer Vision' 카테고리의 다른 글
| Linear Filters (0) | 2020.10.08 |
|---|---|
| Color (0) | 2020.09.29 |
| Radiometry (0) | 2020.09.18 |
| Camera Calibration (0) | 2020.09.13 |
| Camera (0) | 2020.09.13 |



