* 이 포스트는 컴퓨터 비젼에 대한 개인 학습용으로 작성한 포스트입니다.
Invariant Features
일반적으로 컴퓨터비젼에서는 3개의 문제가 존재한다.
1. Detection : 특징 포인트를 어떻게 찾을 것인가?
2. Description : robust하게 local region을 설명하는가?
3. Matching : 신뢰성있게 각 점을 일치시킬 수 있는가?
Feature는 Roation, Scale, Affine, Photometic에 invariant해야함
앞에서 포스팅한 Harris corner detector는 rotation, affine에 invaraint하지만 scale변화에는 그렇지않음
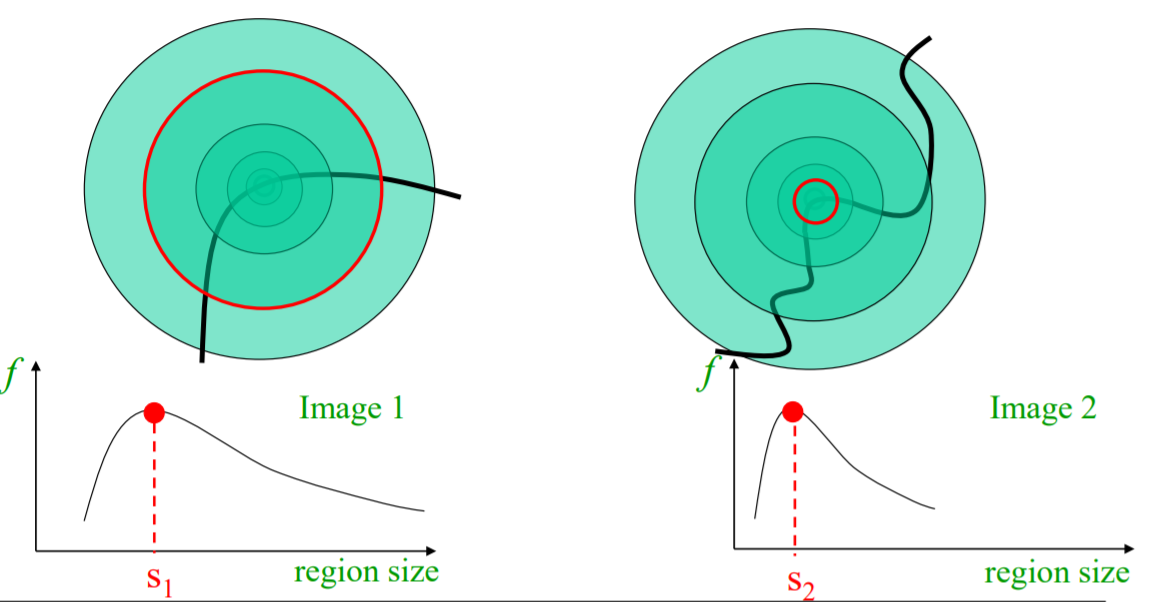
Harris corner detector와 같은 detector를 사용했을 때, scale의 변화에 따라 response를 나타낼 수 있다. 이때, response가 maximum이 되는 scale 값을 찾을 수 있다.
LoG Detector
Edge/Corner를 detect하기위해 laplacian of gaussian filter를 사용한다는 것을 전 포스팅에서 설명하였다. $\sigma $의 값에 따라 scale을 달리하는 것으로 할 수 있다. 하지만, 아래 그림에서 한쪽 넓이가 $1 \over {\sigma \sqrt{2\pi}}$가 되어 $\sigma$가 커질수록 넓이가 작아진다.

이를 보정하기 위해 아래 식으로 normalize를 진행한다.
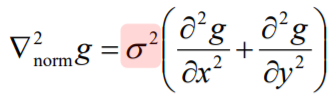
$\sigma$에 따라 LoG operator를 적용한 결과를 stack할 수 있다. 그 결과, 3차원 형태의 데이터가 형성된다. 그리고 scale에 따라 local maxima에 해당하는 부분을 찾으면 강하게 나타나는 feature이라 할 수 있다.

아래 그림은 위의 매커니즘을 거친 결과이며, feature point와 scale을 함께 표기한 영상이다.
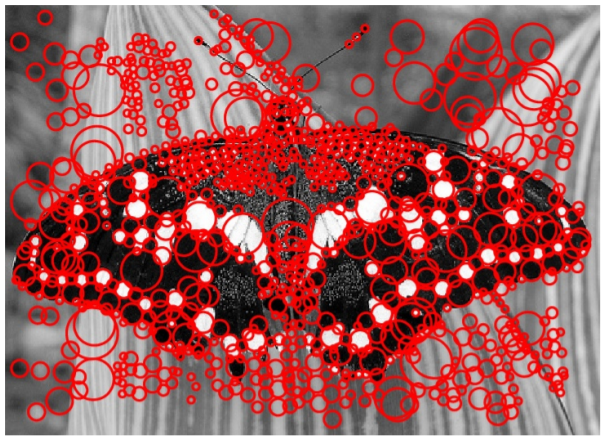
위에서 LoG filter를 사용하였다. Laplacian of Gaussian에서 계산량을 줄이고 approximate한 DoG filter를 사용하기도 한다. 식은 아래와 같다. 이 filter도 rotation, affine등에 불변이다.

SIFT Algorithm
: Scale Invariant Feature Transform Algorithm
위에서 설명한 것과 비슷하게, DoG scale space에서 scale에 따라 extrema 지점을 찾는 것이 중요하다. 하지만, scale 변화는 알고리즘 상에서 직접 down sampling한 것이므로 discrete하기 때문에 정확한 값을 가지지 않는다.

이를 해결하기 위해, Taylor expansion을 통해 아래와 같이 식을 approximation할 수 있다.

이를 미분하여 아래 식을 유도할 수 있고, 이 식을 이용하면 정확한 값을 추론가능하다.

Hessian matrix에서 고유값 비율에 따라 corner인지, edge인지 여부를 파악할 수 있다는 것을 앞에서 설명하였다. 아래 식처럼 Trace와 Determinant를 이용해 Ratio를 정의하여 edge가 아닌 corner에 대한 point를 남겨 놓을 수 있다.
SIFT algorithm에서 일반적으로 r = 10을 사용한다.

Affine Adaptation method
: Affine 변화에도 invariant한 detection이 가능한가?
-> Second order moment를 이용하여 elipse를 잡고 이것이 circle이 되도록 image를 warping시킨 다음에 maxima를 찾음 (이를 반복)
1. Detect keypoints in a multi-scale space
2. Automatically select the scales
3. Adapt affine shape based on second order moment matrix
4. Refine point location
아래는 Affine 변화까지 고려한 feature point들이다.

Affine normalization
위의 방법으로 Affine 변화가 일어난 부분을 Normalization하는 것이 가능하다.

Eliminating rotation ambiguity
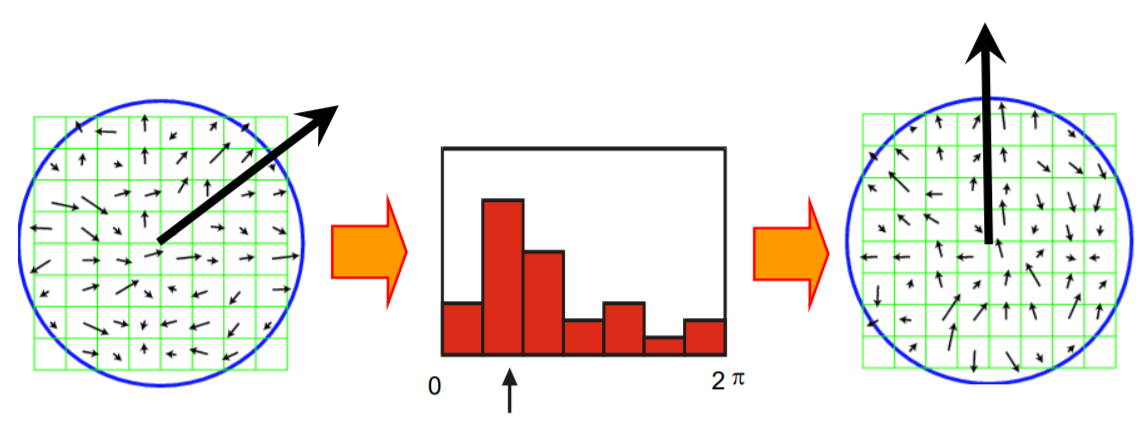
Orientation histogram을 만들 수 있고, 이를 통해 어디로 align시켜야하는지 알 수 있다. 이를 통해 방향또한 normalization이 가능하다.
Affine-Invariant Feature Extraction (Descriptor)
최종적으로, align된 descriptor를 추출할 수 있고, 이것이 같은 region에 대한 descriptor인지 비교를 할 수 있다. (matching 할 수 있음을 시사)
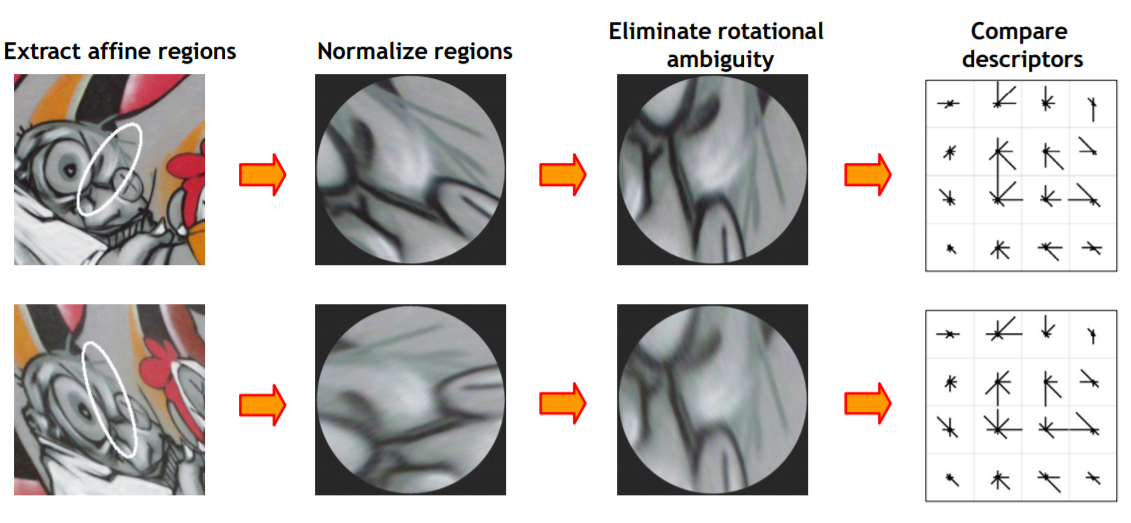
Rotation Invariant Descriptor
matching하기 위해서, rotation이나 scale등에 invariant한 descriptor가 생성되어야함
위에서 추출한 feature을 중심으로 4x4 sub patch를 생성한다. 그리고 각 cell당 gradient orientation을 계산한다. (8개)
최종적으로, 4x4x8 = 128 dimension의 vector descriptor가 생성된다. (4, 8 값은 practical 실험결과로 결정)
-> 위에서 언급한 것처럼, 가장 세기가 큰 orientation을 기준으로 방향을 align (normalize)하는 과정이 필요

Feature matching - Correspondence
최종적으로 두 영상에서 feature matchig을 해야한다.
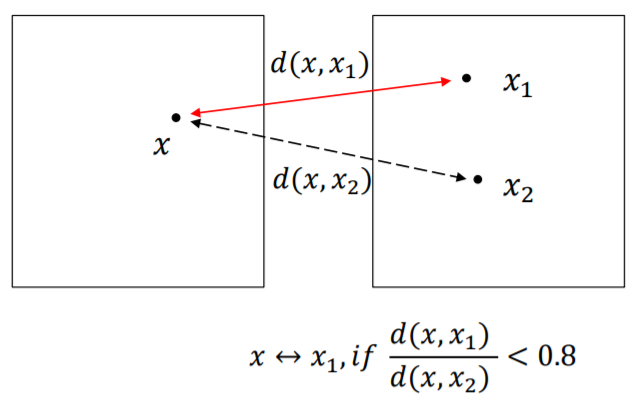
위에서 $x$에 제일 가까운 feature를 $x_1$, 두번째로 가까운 feature를 $x_2$라 할 때, 두 개사이의 거리 비율이 0.8 미만일 때, 제대로 match되었다고 판별한다.
'Basic Learning > Computer Vision' 카테고리의 다른 글
| Homography & Alignment (0) | 2020.10.27 |
|---|---|
| Fitting (0) | 2020.10.25 |
| Scaled Representations : Image Pyramid (0) | 2020.10.08 |
| More Features (0) | 2020.10.08 |
| Edges (0) | 2020.10.08 |



