* 이 포스트는 알고리즘의 기초에 대한 개인 학습용으로 작성한 포스트입니다.
Mergesort
array를 반으로 나누어 2개의 array를 만든다.
각 array에 대해 recursive하게 sort를 진행한다.
Sort된 두개의 array를 이용하여 하나의 큰 sorted array로 merge한다.

두개의 array가 sort되었다고 가정하므로, 각 array에 대해 왼쪽에서 오른쪽으로 진행하면서 comparison을 진행하면된다. 그 결과, merge에 $O(n)$의 시간이 걸린다.
Mergesort recurrence

n을 2의 지수승이라 하면 다음과 같다.

Time complexity : $O(nlogn)$
Proof by recursion tree
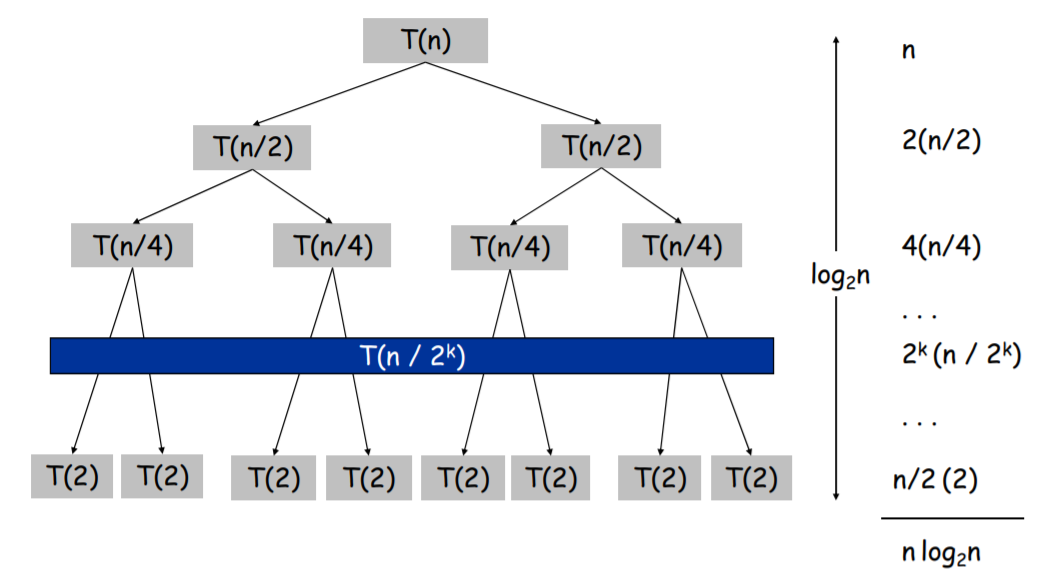
Recursion을 tree로 표현할 수 있다. Depth는 logn이고, 각 level에서 merge에 소요되는 시간은 n이 걸린다. 그러므로 $O(nlogn)$의 time complexity를 가진다.
Proof by induction
n = 1일 때는 만족.
n일 때 time complexity는 $O(nlogn)$을 만족하다 가정하자, 2n 때 time complexity는 $O(2nlog2n)$을 만족함을 보이자.

Counting Inversions
순서가 있는 데이터들이 나열되어 있을 때, 대소 관계가 뒤집혀있는 것을 inversion이라 한다. Counting inversions 문제는 list의 inversion 개수를 계산하는 문제이다. 아래 그림에서는, 12345 순서로 나열되어 있어야하는데, 3-2, 4-2 두 개가 순서를 위반하므로 inversion 개수는 2개이다.

Divide and Conquer : Implementation

Sort-and-Count(L) 함수는 inversion 개수 r, sorted list L을 반환한다. 2개의 sorted list가 주어졌을 때, inversion 개수는 다음 방식으로 계산한다.

위의 예제에서, 전체 list를 blue list, green list로 나누었다. Inversion 개수는 blue-blue간의 inversion, green-green간의 inversion, blue-green간의 inversion 개수를 합한 것이다. 이때, 자기 자신의 inversion은 주어지므로, blue-green 간의 inversion 개수를 구하는 것이 중요할 것이다.
Blue, green list 모두 sort되어 있으므로, green list의 한 원소를 기준으로, 해당 원소보다 큰 원소의 개수를 blue list에서 찾으면 된다. 2를 선택했을 경우, blue list에서 첫번째 원소가 3이므로 뒤의 원소들은 3보다 크기 때문에 모두 2보다 클 것이다. 그러므로 2에 해당되는 inversion은 6개이다. green list에서 11을 선택했을 경우, blue list의 선택을 14까지 이동한다. 그러고 뒤의 원소 역시 크므로 11의 inversion은 3개이다.
이런 방식으로 진행하면, 다시 뒤돌아오는 경우는 없으므로, merge에 $O(n)$의 시간이 걸린다.
최종적으로 위 알고리즘의 Time complexity는 $O(nlogn)$이다.
'Basic Learning > Algorithm Design' 카테고리의 다른 글
| Dynamic Programming (0) | 2020.11.09 |
|---|---|
| Closest Pair of Points (0) | 2020.10.22 |
| Huffman Coding (0) | 2020.10.17 |
| Minimum Spanning Tree & Clustering (0) | 2020.10.08 |
| Optimal Caching & Shortest Paths in Graph (0) | 2020.10.07 |



